드디어 랜덤 프로세스입니다. 우리가 비록 각종 분포들 (정규, 베르누이, 푸아송, 감마, 카이제곱, 균등, ...) 을 생략하고 왔지만 이 분포는 여러분들과 제가 필요할 때 보아서 이해할 수 있을 것이라 생각하고 나가겠습니다.

랜덤 프로세스가 무엇일까요? 한국말로 무식하게 번역하면 '무작위 절차'라고 할 수 있을 겁니다. 무언가를 주면 무작위로 무언가가 나오는 절차라고 생각할 수 있습니다. 그리고 실제로 그렇습니다. 그럼 '작위적 절차'라는 것은 무엇일까요? 그것은 함수라고 생각합니다. y=f(x) 에서 X={a, b, c} 이고 Y={p, q, r} 이라 하면 Sample space (혹은 domain) 에서 a를 주면 언제나 결과는 q입니다. 이 관계는 시간 불변인 관계이죠. 그러나, 무작위 절차 즉 랜덤 프로세스에서는 이 공리가 깨집니다. Sample space 에서 같은 것을 주었다고 해도 결과가 다를 수 있습니다. 이 원인이 시간이라고 한다면 이 관계는 시간에 간섭되고 있는 것입니다.

이 경우 우리는 작위적 절차처럼 '함수'라는 것으로 직관적인 정형화를 할 수가 없습니다. (모든 랜덤 프로세스에 대해 최적화된 정형화를 직관적으로 할 수 있다면 지금 당장 취업을 하세요. 물론 직관을 증명해야 하겠지만, 증명 시간이 짧고 가성비가 좋은 랜덤 프로세스를 만들 수 있기 때문에 회사가 좋아할 겁니다. 한 사람이 일을 하는데 적은 시간이 걸린다는 것은 같은 월급을 주고도 더 많은 일을 시킬 수 있다는 것이니까 회사 입장에선 마다할 이유가 없죠.) 그러나 랜덤이라는 관계를 성립시키기 위해서는 주어진 결과를 represent 하면서도 어떻게든 랜덤'처럼 보이도록' 해야 합니다. 그리고 이 랜덤처럼 보이도록 만든 시간 의존적인 식은 우리가 제시하는 분포에도 맞아야 합니다.

이것을 직관적으로 하기 어렵기 때문에, 우리는 랜덤 프로세스들을 여러 case에 따라 분류할 것이며, 각 case에 대한 효과적인 식을 drive하기 위해 노력할 것입니다. 그리고 이 효과적인 식 (계산 수행 시간이 짧고, 필요한 정보가 적고 등등 효과를 논하기 위한 요소들이 있습니다.) 을 만들고, 더 개선하기 위해 지금부터 랜덤 프로세스를 배워봅시다.

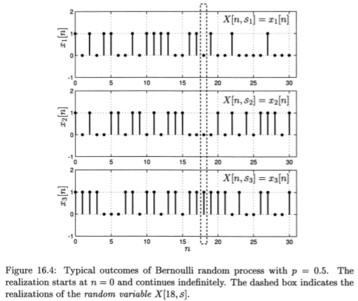
(출처 : Intuitive Probability and Random Process using MATLAB)

앞으로 쓰일 notation들을 간단히 알아보기 위해 쉬운 랜덤 프로세스를 하나 가져왔습니다. 위 그래프들은 0부터 30의 자연수를 caring sample space로 하여 (실제 sample space는 infinite하지만 31이후로는 don't care한 경우입니다.) 이로부터 Bernoulli random process (p = 0.5) 를 수행하였습니다. 3개의 ensemble (그래프의 수가 3개이다.) 을 얻었으며, 그 결과를 위에 기록하였습니다.

앞으로 s represents s_i 는 i번째 앙상블 s_i 에 대하여 모든 앙상블을 s 라고 말하는 것을 의미합니다. 따라서 이 경우 X[N, S]에 대하여 S=s 이면 모든 앙상블을 지정합니다. 또한 N=n 이면 모든 sample space element 를 지정합니다. 예를 들어 E[X[n, s]] 이면 모든 앙상블, 모든 sample space element 에 대한 평균을 의미합니다. 위에서 보면 점선으로 표시된 영역이 X[18, s] 즉 N=18 인 sample space element 에 대한 모든 앙상블을 지정하고 있는 영역을 표시하고 있음을 알 수 있습니다.

일반적으로, n이나 t 등 sample space element들은 'time' 즉 시간이라고 합니다. 간단히 생각해서, N=20 이면 20 단위 시간이라는 표현과 같다는 것입니다.

우리는 앞으로 이 notation들을 이용해 여러 case들을 정의해 나갈 것입니다.

위 예시는 Bernoulli random process 였습니다. 그런데 이것을 잘 생각해보면 time(sample space)이 항상 discrete 하다고 생각할 수는 없습니다. 마찬가지로 value (여기서는 x_i[n] (i는 i번째 앙상블을 의미함), (x_i[n] = X[n, s_i])) 또한 항상 discrete 하다고 생각할 수 없습니다. 이 생각으로부터 우리는 DTDV, DTCV, CTDV, CTCV 를 정의합니다.

DTDV: Discrete Time, Discrete Value

DTCV: Discrete Time, Continuous Value

CTDV: Continuous Time, Discrete Value

CTCV: Continuous Time, Continuous Value

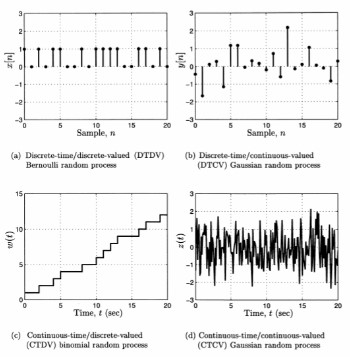
예시는 이렇습니다. 간단히 생각하면 discrete와 continuous의 차이는 최소 단위를 정할 수 있는가 없는가의 차이입니다. (a)를 보면 time과 value 모두 1이라는 최소 단위를 정할 수 있습니다. (b)는 time에 대해서는 가능하지만 value는 실수 범위이기 때문에 최소 단위를 지정할 수 없습니다. (c)는 time의 어디서 step이 일어나는지 모르고 따라서 최소 단위가 없지만 value는 1이라는 최소 단위를 지정할 수 있습니다. (d)는 그냥 없네요.

지금까지 앞으로 쓰일 notation들과 정의역(time)-공역(value)의 연속성 여부에 따라 DTDV, DTCV, CTDV, CTCV에 대해 정의해보았습니다. 다음부터는 잘 알려진 특성에 따라 앞서 연구한 수학자들이 밝혀 놓은 case들을 따라가 보겠습니다.

합성곱은 여러분이 공대 혹은 수학을 조금만 하셔도 미분방정식, 신호처리이론, 물리, 전자기학 등등 많은 분야에서 등장하기 때문에 여기서 한 번 다루고 넘어가는 것이 좋을 것 같습니다.

사실 합성곱에 대해서 그 정의는 위키피디아만큼 완벽하게 설명된 곳이 없습니다.

https://ko.wikipedia.org/wiki/%ED%95%A9%EC%84%B1%EA%B3%B1

위키를 보면, 합성곱은 '하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자'라고 정의되어 있습니다. 실제로 오른쪽의 도식을 보면, 그러한 특성을 잘 확인할 수 있습니다.

확률변수의 개념 중 함수들, 정확하게는 CDF와 PDF를 이 함수로 볼 때, 그 합성곱에 대한 연산을 정의할 수 있습니다. CDF의 convolution은 독립인 확률분포 X와 Y로부터

PDF의 convolution은 역시 독립인 확률분포 X와 Y로부터 구한 CDF를 미분하여

위와 같이 구할 수 있습니다.

확률변수의 '합'이 어떻게 합성'곱'이 되는 걸까요? 수식으로는 납득이 되지만, 도저히 마음속으로는 이해가 안되시는 분들을 위해서 설명해드리겠습니다.

위키피디아를 잘 읽어보면, 사실 합성곱은 '곱'은 아니고 겹친 부분의 적분입니다. 곱의 형태가 된것은 X와 Y가 독립이었기 때문에 조건부 형태의 joint PDF가 아닌 두 개의 분리된 PDF들의 곱이 된 것, 단지 그 이유입니다. 그러니 X의 PDF와 Y의 PDF가 곱해진 것을 그냥 '겹쳐진 부분에 대한 함수'로 보아도 됩니다.

그렇다면 a는 무엇일까요? a는 X의 PDF의 2*(축)의 위치입니다. 무슨 소리냐 하면, 예를 들어 X와 Y가 같은 분포, 이른바 IID (독립임은 앞에 언급했으므로) 라고 합시다. 그렇다면 곱해지는 함숫값에 해당하는 정의역의 위치는 y와 a-y 입니다. y 에서 -y가 된 것은 전치를 의미하므로 전치가 되는 축을 구하기 위해 y = a-y 라 하면 y = a/2 가 됩니다. 이 때의 y를 '축'이라고 합니다.

예를 들어 a=1 이면 축은 y=1/2 인 것이죠.

IID인 두 분포 X와 Y의 평균이 m이라면 a=2m 일 때 합의 분포 X+Y가 최댓값을 보임은 쉽게 알 수 있습니다.

왜 이런 겹치는 형태가 될까라고 의아해 하실 수도 있습니다.

그것은 한 가지 예시로 쉽게 알려드리겠습니다.

철수와 영희가 영호에게 영호가 내는 문제를 맞추면 50원씩을 각각 받기로 했습니다. 철수와 영희는 문제를 잘 몰랐고, 할 수 없이 맞다, 틀리다 중 하나를 고르는 문제를 내었습니다. 이 때 철수의 돈의 획득 분포는 p=0.5인 베르누이 확률변수이며 영희도 마찬가지입니다. 그렇다면 두 사람이 받을 수 있는 돈의 합은 0원, 50원, 100원 중 하나입니다.

이제 겹치는 것의 의미를 보여드리겠습니다.

영희가 틀린 것은 흰색 별, 맞은 것은 검은 별, 철수가 틀린 것은 흰색 동그라미, 맞은 것은 검은 동그라미라고 합시다.

      ☆★

○●

철수와 영희가 떨어져 있으므로 (다시 언급하지만, 곱의 형태가 된것은 다름이 아니고 조건부가 '독립'이기 때문입니다. 따라서 아래와 같은 표현을 쓸 수 있습니다.)

이제 철수의 함수를 한칸 옆으로 옮기면,

      ☆★

   ○●

     ☆★

     ○●

     ☆★

        ○●

이때 맞은 사람 수를 기준으로 전체 확률을 합하면 0.25, 0.5, 0.25로 각각 0원, 50원, 100원의 확률임을 알 수 있습니다. 합성곱은 연속확률변수에서 적용되므로 베르누이 분포대신 균등분포를 사용하면 이와같은 삼각형 꼴의 연속한 분포 (삼각분포) 를 얻을 수 있습니다.

다음 글에서는 랜덤 프로세스에 대해 알아보겠습니다.